
Machine Learning in Construction: How Clustering Data Can Improve Processes (part 2 of 2)
Director, Enstoa
In the previous article we gave you an introduction to machine learning in construction, and we mentioned that machine learning can be broken into two broad categories: supervised learning and unsupervised learning. While supervised learning has an output or response variable that analysts are focused on (for example, a cost performance metric), unsupervised learning relies on having no response variable – the objective is to simply explore the data available.
Unsupervised methods, such as clustering data, are often employed during the preliminary or exploratory phases of construction projects.
What is clustering?
A clustering algorithm, in general, aims to segment or partition data, such that similar observations are grouped together. To put it differently, the more similar two observations are, the more likely they are to find themselves in the same group.
Think of it this way: Imagine you have a number of objects in a basket. Each item has a distinct set of features (size, shape, color, etc.). Imagine now that you have been tasked with grouping each of the objects in the basket. A natural first question to ask is, ‘on what basis will I group these objects?’ Perhaps size, shape, or color.
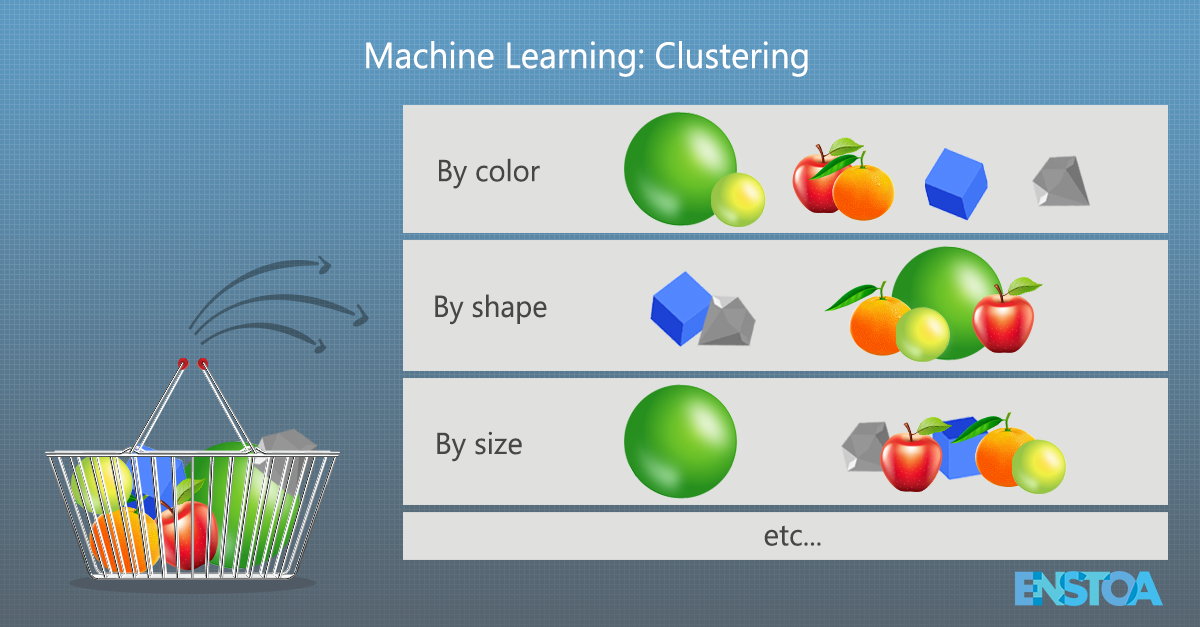
Figure 1: Clustering involves grouping objects according to their similarities, like in this basket example.
Or perhaps not. The answer you choose may depend on many factors, including how many objects there are, how similar (or different) they are, or even how heavy certain objects are. It isn’t at all obvious which grouping criterion you should choose. Often, the best answer is to group the objects on the basis of all their features. As the basket grows larger and the number of objects increases, the task of grouping them becomes increasingly complex – there can be as many ways to group the objects as there are objects in the basket!
Simply put, clustering algorithms are helpful tools in managing unwieldy baskets.
As noted above, clustering methods fall into the unsupervised learning category; there is no output variable we want to describe or outcome we want to predict, we simply want to explore the data at hand.
In K-Means clustering (where the goal is to create K-many distinct and non-overlapping groups within a data set), partitioning is accomplished by minimizing the sum of the mean squared error between each observation and the exact center point (or centroid) of the group to which that observation belongs.
K-Means clustering is by no means the only way to group data; there are many techniques one can employ to arrive at a cluster. A clustering analysis can be a good starting point when examining a new data set as it may help identify hidden structures deep in the data.
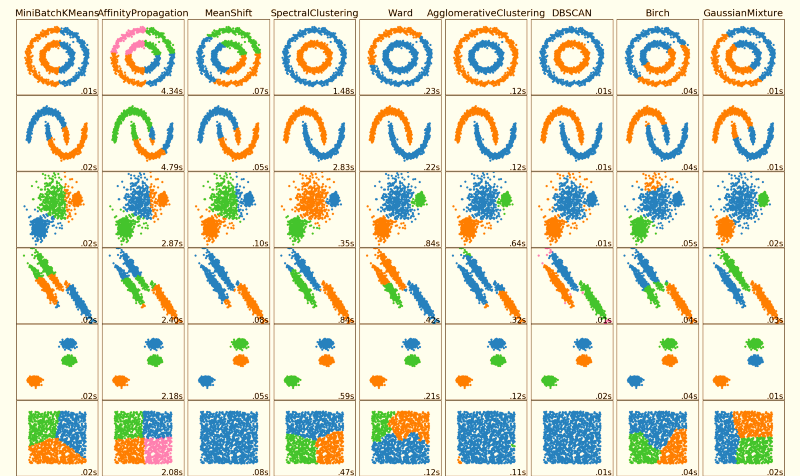
Figure 2: Various clustering algorithms applied to characteristically distinct data sets. Experience and experimentation work hand in hand to narrow the question of which techniques to apply to which types of data.
How can clustering algorithms be applied?
A fundamental activity in data science is data exploration. In practical terms, a data scientist approaches his or her dataset with an open mind and the freedom to creatively investigate relationships within the data. Recently, we at Enstoa embarked on a project that exemplifies data exploration.
We were tasked with analyzing project management data with reference to historic project records of a set of in-house project managers. The objective was to develop a strong understanding of present and historical workloads to underpin a predictive analytic model that was also in development. In exploring the data, six key variables were identified that fit broadly into two categories: the types of projects each project manager typically manages, and the value of projects assigned to each project type.
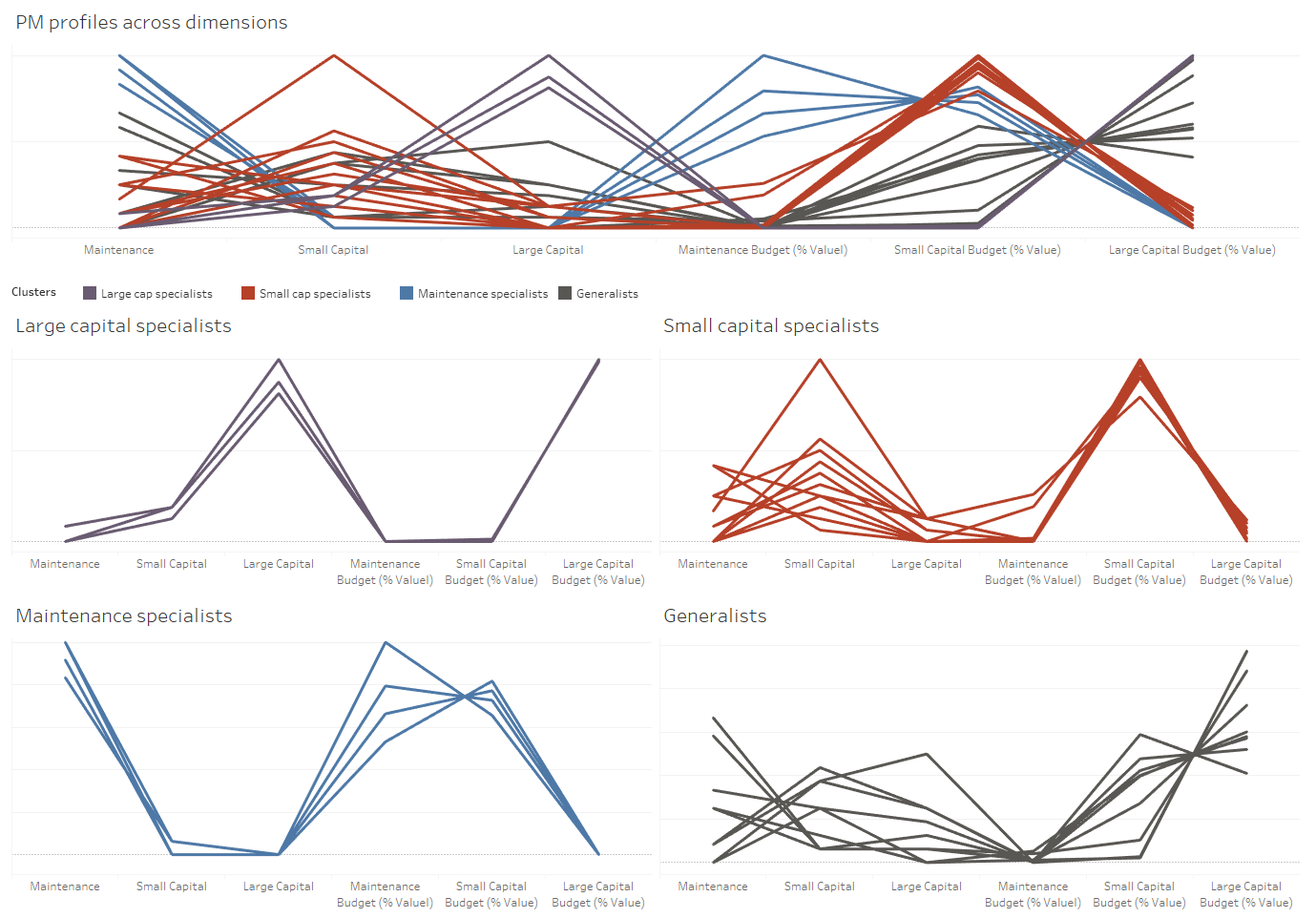
Figure 3: Un-clustered data of 30 project managers mapped across 6 dimensions
After normalizing the data, a clustering analysis was performed (as a technical aside, normalization and/or data scaling is crucial when applying clustering algorithms). The project managers were assigned to groups based on how similar they were, among the six identified dimensions, to other project managers. The more similar two project managers were, the more likely they were to find themselves in the same group. The present sample contains data on 30 individual project managers.
Given this set, one could group the observations into as many as 30 clusters (in such a case, each individual would reside in their own cluster) and as few as a single cluster (where everyone would be in the same group). There is a delicate balance to choosing the right number of groupings: too many groups and the profiles become too granular, too few and the exercise offers no additional insights at all. In technical terms, we aim to minimize the ‘mean squared error’ while not overfitting the data.
One of the tools available to help determine the right number of grouping is called an elbow curve. An elbow curve plots the clustering score (i.e., a transformed measure of the mean squared error) against the number of clusters (how many groupings were chosen). Highlighted in Figure 4 below is an inflection in the curve (the 'elbow'). At this elbow, there is very little reduction in error for each additional grouping introduced to the data. This helps a practitioner identify how many clusters to choose. Figure 4 suggests that we should examine cases with between 3 and 6 clusters.
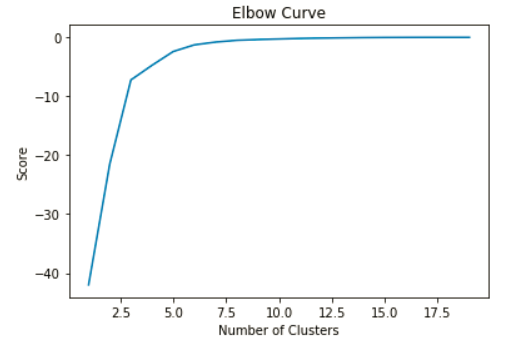
Figure 4: An elbow diagram can help determine K in “K-Means”. In this case, the area of interest is between 3 to 6 clusters.
What can we learn from clustering analysis?
Setting K equal to 4, the present dataset clusters nicely around four groupings. We have mapped the four groups to business categories (Large Capital specialists, Small Capital specialists, Maintenance specialists, and Generalists). These categories can be thought of as a data driven ‘sub-type’ of the Project Manager role in the organization.
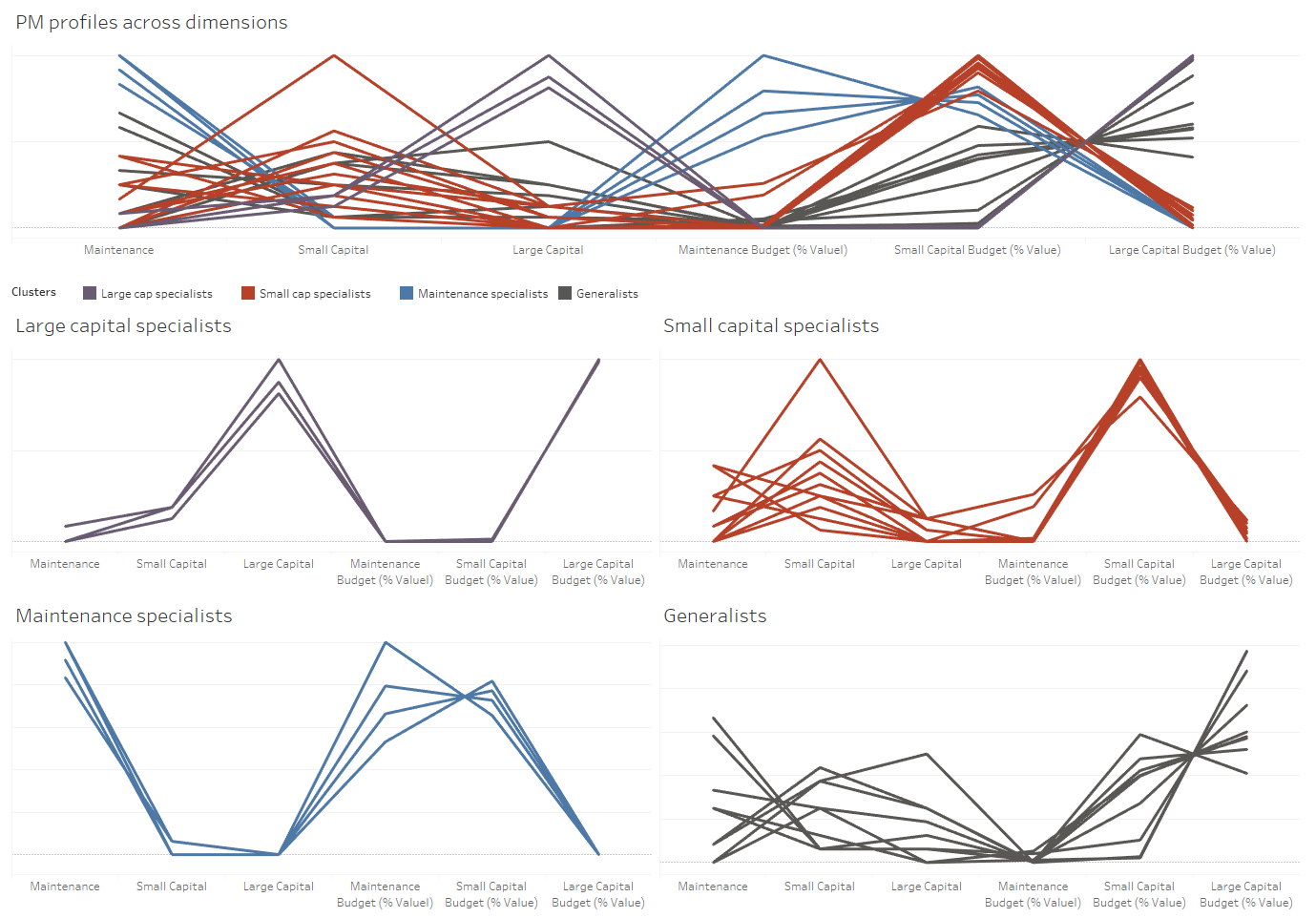
Figure 5: Post-Clustered Data (K-Means, K = 4). Each line represents a PM and each color is a cluster.
Why is this important? Because employing these kinds of analyses can provide a validity check on long-held assumptions and act as an input variable for resource planning.
Consider the following applications of this data:
Performance reviews
Instead of all project managers being reviewed as a single team, we could use this clustering analysis to develop a better focused peer group.
Career Development
How a project manager’s individual profile changes over time could be leveraged to target training and support for career development.
Resource forecasting
Looking towards the horizon of the capital plan, these clusters act as resource profiles, providing portfolio planners with better fidelity into future resource capacity needs.
In Conclusion
From the clustering example above, the findings likely wouldn’t surprise a portfolio director who knows his team. Rather, the value in this example is that it provides a data-driven framework that can be applied to several organization processes to enhance planning and management. The key take-away is that there is untapped potential in your data – potential that can be used to enhance and improve “the work.”
Clustering is one example of how machine learning can help organizations improve processes by using meaningful data to inform changes. While embracing machine learning can be an overwhelming process for an organization, starting with a small pilot project can help pave the way for inspiring an entire organization to embrace the power of machine learning.
In the previous article we gave you an introduction to machine learning in construction, and we mentioned that machine learning can be broken into two broad categories: supervised learning and unsupervised learning. While supervised learning has an output or response variable that analysts are focused on (for example, a cost performance metric), unsupervised learning relies on having no response variable – the objective is to simply explore the data available.
Unsupervised methods, such as clustering data, are often employed during the preliminary or exploratory phases of construction projects.
What is clustering?
A clustering algorithm, in general, aims to segment or partition data, such that similar observations are grouped together. To put it differently, the more similar two observations are, the more likely they are to find themselves in the same group.
Think of it this way: Imagine you have a number of objects in a basket. Each item has a distinct set of features (size, shape, color, etc.). Imagine now that you have been tasked with grouping each of the objects in the basket. A natural first question to ask is, ‘on what basis will I group these objects?’ Perhaps size, shape, or color.

Or perhaps not. The answer you choose may depend on many factors, including how many objects there are, how similar (or different) they are, or even how heavy certain objects are. It isn’t at all obvious which grouping criterion you should choose. Often, the best answer is to group the objects on the basis of all their features. As the basket grows larger and the number of objects increases, the task of grouping them becomes increasingly complex – there can be as many ways to group the objects as there are objects in the basket!
Simply put, clustering algorithms are helpful tools in managing unwieldy baskets.
As noted above, clustering methods fall into the unsupervised learning category; there is no output variable we want to describe or outcome we want to predict, we simply want to explore the data at hand.
In K-Means clustering (where the goal is to create K-many distinct and non-overlapping groups within a data set), partitioning is accomplished by minimizing the sum of the mean squared error between each observation and the exact center point (or centroid) of the group to which that observation belongs.
K-Means clustering is by no means the only way to group data; there are many techniques one can employ to arrive at a cluster. A clustering analysis can be a good starting point when examining a new data set as it may help identify hidden structures deep in the data.

How can clustering algorithms be applied?
A fundamental activity in data science is data exploration. In practical terms, a data scientist approaches his or her dataset with an open mind and the freedom to creatively investigate relationships within the data. Recently, we at Enstoa embarked on a project that exemplifies data exploration.
We were tasked with analyzing project management data with reference to historic project records of a set of in-house project managers. The objective was to develop a strong understanding of present and historical workloads to underpin a predictive analytic model that was also in development. In exploring the data, six key variables were identified that fit broadly into two categories: the types of projects each project manager typically manages, and the value of projects assigned to each project type.

After normalizing the data, a clustering analysis was performed (as a technical aside, normalization and/or data scaling is crucial when applying clustering algorithms). The project managers were assigned to groups based on how similar they were, among the six identified dimensions, to other project managers. The more similar two project managers were, the more likely they were to find themselves in the same group. The present sample contains data on 30 individual project managers.
Given this set, one could group the observations into as many as 30 clusters (in such a case, each individual would reside in their own cluster) and as few as a single cluster (where everyone would be in the same group). There is a delicate balance to choosing the right number of groupings: too many groups and the profiles become too granular, too few and the exercise offers no additional insights at all. In technical terms, we aim to minimize the ‘mean squared error’ while not overfitting the data.
One of the tools available to help determine the right number of grouping is called an elbow curve. An elbow curve plots the clustering score (i.e., a transformed measure of the mean squared error) against the number of clusters (how many groupings were chosen). Highlighted in Figure 4 below is an inflection in the curve (the 'elbow'). At this elbow, there is very little reduction in error for each additional grouping introduced to the data. This helps a practitioner identify how many clusters to choose. Figure 4 suggests that we should examine cases with between 3 and 6 clusters.

What can we learn from clustering analysis?
Setting K equal to 4, the present dataset clusters nicely around four groupings. We have mapped the four groups to business categories (Large Capital specialists, Small Capital specialists, Maintenance specialists, and Generalists). These categories can be thought of as a data driven ‘sub-type’ of the Project Manager role in the organization.

Why is this important? Because employing these kinds of analyses can provide a validity check on long-held assumptions and act as an input variable for resource planning.
Consider the following applications of this data:
Performance reviews
Instead of all project managers being reviewed as a single team, we could use this clustering analysis to develop a better focused peer group.
Career Development
How a project manager’s individual profile changes over time could be leveraged to target training and support for career development.
Resource forecasting
Looking towards the horizon of the capital plan, these clusters act as resource profiles, providing portfolio planners with better fidelity into future resource capacity needs.
In Conclusion
From the clustering example above, the findings likely wouldn’t surprise a portfolio director who knows his team. Rather, the value in this example is that it provides a data-driven framework that can be applied to several organization processes to enhance planning and management. The key take-away is that there is untapped potential in your data – potential that can be used to enhance and improve “the work.”
Clustering is one example of how machine learning can help organizations improve processes by using meaningful data to inform changes. While embracing machine learning can be an overwhelming process for an organization, starting with a small pilot project can help pave the way for inspiring an entire organization to embrace the power of machine learning.




